Abstracts

Kirkwood-Buff integrals from molecular simulation

Noura Dawass   Technical University Delft, Delft, The Netherlands

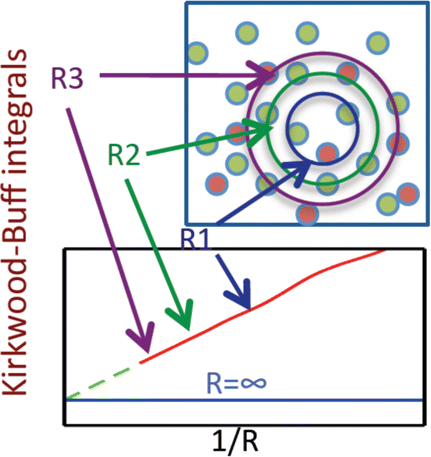
The Kirkwood-Buff (KB) theory provides a rigorous framework to predict thermodynamic properties of isotropic liquids from the microscopic structure. Several thermodynamic quantities relate to KB integrals, such as partial molar volumes and partial derivatives of chemical potential with respect to composition. KB integrals are expressed as integrals of RDFs over volume but can also be obtained from density fluctuations in the grand-canonical ensemble. KB integrals are defined for infinite and open systems while molecular simulations access finite systems. Various methods have been proposed to estimate KB integrals from molecular simulation. One of the most practical approaches has been recently proposed by Schnell et al. (2013), where an expression for KB integrals of finite volumes was derived. These integrals are computed from RDFs of open and finite volumes embedded in a larger simulation box (reservoir). The KB integrals of finite volumes are computed for subvolumes with different sizes. The scaling of KB integrals with the inverse size of the subvolumes is used to extrapolate to the thermodynamic limit to find KB integrals of infinite systems. To accurately estimate KB integrals from molecular simulation using this approach three effects have to be studied: system-size effects, RDFs-related effects, and subvolumes shape effect. This talk will provide answers on to how deal with such effects.

Kirkwood-Buff Integrals and Nano-Thermodynamics: application to chemically constrained systems

Jean-Marc Simon   ICB, Université de Bourgogne, Dijon, France

Small systems cannot be described by classical thermodynamics. One reason is that the surface area becomes important, in contrast to the case for systems in the thermodynamic limit. The increased experimental interest in nanosized systems, has created a demand on the theoretical side. Our aim has been to find a systematic description of the thermodynamic properties of small systems; their size and shape-dependence in particular. Thereby we hope to improve the understanding and modelling ability of such systems. The thermodynamics of small systems (also called nanothermodynamics) was first developed by T. L. Hill [1] in the sixties. It gives a general background to systematically express thermodynamic properties in terms of system size [2]. During the last 5 years we applied this approach to the analysis of molecular dynamics simulations and we developed new efficient tools to compute thermodynamic properties like partial molar quantities that can be hardly accessible by other methods. The method was tested on different system types [2, 3, 4, 5, 6, 7]: Lennard-Jones mixtures, ternary molecular systems, reactive mixtures (2H=H2), CO adsorbed on graphite,... These results validate the use of the thermodynamics of small systems for molecular systems and clearly show that they are consistent both with the Kirkwood-Buff approach [3, 4, 8, 9] and Gibbs' thermodynamics for a surface [10]. Beyond the application to molecular simulated data, this new approach opens new ways to study systems were the individual particle sizes are large compared to the system size. During the presentation I will present the way we applied nanothermodynamics for the benefit of the analysis of molecular simulations, and I will put a focus on the analysis of chemically constrained systems.
[1] T. L. Hill. Thermodynamics of small systems. Part 1, Benjamin, New York, 1963.
[2] Thermodynamics of small systems embedded in a reservoir: a detailed analysis of finite size effects S. K. Schnell, T. J. H. Vlugt, J.-M. Simon, D. Bedeaux, S. Kjelstrup, Mol. Phys. 110, 1069 (2012)
[3] Kirkwood-Buff Integrals for Finite Volumes, P. Kruger, S. K. Schnell, D. Bedeaux, S. Kjelstrup, T. J. H. Vlugt, J.-M. Simon, J. Phys. Chem. Lett., 4, 235 (2013)
[4] How to apply Kirkwood-buff theory of individual species in salt solutions, S. K. Schnell, P. Englebienne, J.-M. Simon, P. Kruger, S. P. Balayi, S. Kjelstrup, D. Bedeaux, A. Bardow, T. J. H. Vlugt, Chemical Physics Letters 582, 154 (2013).
[5] Diffusion Coefficients from molecular dynamics in binary and ternary mixtures, X. Liu, S. K. Schnell, J. M. Simon, P. Kruger, D. Bedeaux, S. Kjelstrup, A. Bardow, T. J. H. Vlugt, Int. J. of Thermophys, 34, 1169 (2013).
[6] Calculation of chemical potential and activity coefficient on two layers of CO2 adsorbed on a graphite surface, T.Trinh, D. Bedeaux, J.-M. Simon, S. Kjelstrup, PCCP, 17, 1226 (2015).
[7] Partial molar enthalpies and reaction enthalpies from equilibrium molecular dynamics Simulation, S. K. Schnell, R. Skorpa, D. Bedeaux, S. Kjelstrup, T. J. H. Vlugt, J.-M. Simon, J. Chem. Phys. 141, 144501 (2014)
[8] Kirkwood-Buff integrals of finite systems: shape effects, N. Dawas, P. Kruger, J.-M. Simon, T.H.Vlugt, Mol. Phys. Mol.phys. 116, 15573 (2018)
[9] Kirkwood-Buff integrals from molecular simulation, N. Dawass, P. Kruger, S.K. Schnell, J.-M. Simon, T.J.H. Vlugt, Fluid Phase Equilibria 486, 21-36 (2019)
[10] Size and shape effects on thermodynamic properties of nanoscale volumes of water, B. Strom, J.-M. Simon, S. K. Schnell, S. Kjelstrup, J. He, D. Bedeaux, PCCP, 19, 9016 (2017).

KBI derived from MD simulations using a polarizable force field

Shuntaro Chiba   Riken, Yokohama, Japan

Kirkwood-Buff Integrals derived from MD simulations using a polarizable force field

The Kirkwood-Buff theory is a powerful tool to study aqueous solutions. The theory provides a link between macroscopic and microscopic views of a solution system via the Kirkwood-Buff integrals (KBI), which can be calculated through thermodynamic data of the solution system and can be calculated using radial distribution functions (RDF) of components of the system. RDFs can be obtained from molecular simulation of the system. A molecular simulation that can reproduce experimentally-derived KBIs would provide molecular level details of the system. However, commonly employed parameter sets (force fields) of small molecules for simulations such as OPLSAA and GAFF are not cut out for reproducing experimental KBIs. To address the weakness, Smith's and other groups have developed parameters of various small molecules by fitting the parameters to experimental KBIs. In this study, instead of resorting to fitting of parameter to experimental KBIs, we derived parameters based on quantum chemical calculation. We employed a polarizable model for description of electrostatic potential of a molecule, while the above-mentioned models employed a single point charge model. We found that the polarizable model improved reproducibility of experimental KBIs. In addition, revising parameters such that they can reproduce pairwise interaction energy of molecules in vacuo further improved the reproducibility of KBIs. This finding would enable systematic parameterization method for simulation of a solution system.

pykbi: an open source Python approach to solving Kirkwood-Buff integrals

Sondre K. Schnell   Assoc. professor, Department of Material Science and Engineering, NTNU, Norway

Pykbi is a python-module built to work with calculating Kirkwood-Buff integrals from radial distribution functions. Even if the importance of correct treatment of open and closed systems has been described in a series of papers, there are still many that don't see the importance of using the correct integration method to calculate the Kirkwood-Buff coefficients from radial distribution functions in closed systems. To make the correct integration and extrapolation readily available, we have implemented the state-of-the-art methods into a python module, and made this publicly available through github.com, and the Python Package Index. The focus has been on flexibility and allowing fast access to the integration methods for all users. In this talk we will look at some of the basic features and uses of pykbi.

Generalization of Kirkwood-Buff integral theory to solids

Peter Krüger   Grad. School of Engineering and MCRC, Chiba University, Japan

Kirkwood-Buff integrals (KBI) theory relates the pair-distribution function of a solution to its thermodynamic properties. So far it has only been applied to liquid solutions, but there is no formal reason why it would not be valid for solid solutions, i.e. crystalline matter, too. After reviewing our recent progress in finite volume KBI theory, I discuss its possible extension to solids. First, using the KBI approach, a new and fast converging method for Madelung sums is described. Second, it is shown that the Scherrer/van Laue formulae for the shape of the Bragg peaks in powder diffraction can readily be derived from a finite volume KBI. Finally, prospects and limitations of obtaining thermodynamic information from KBI in solids are discussed.